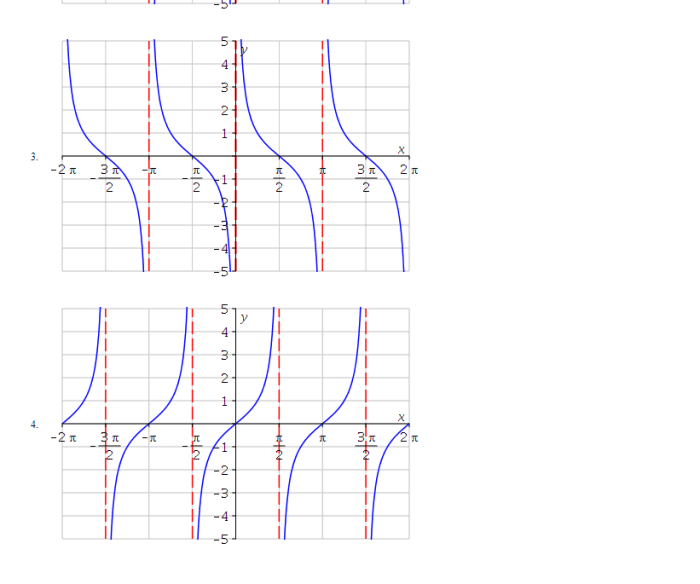
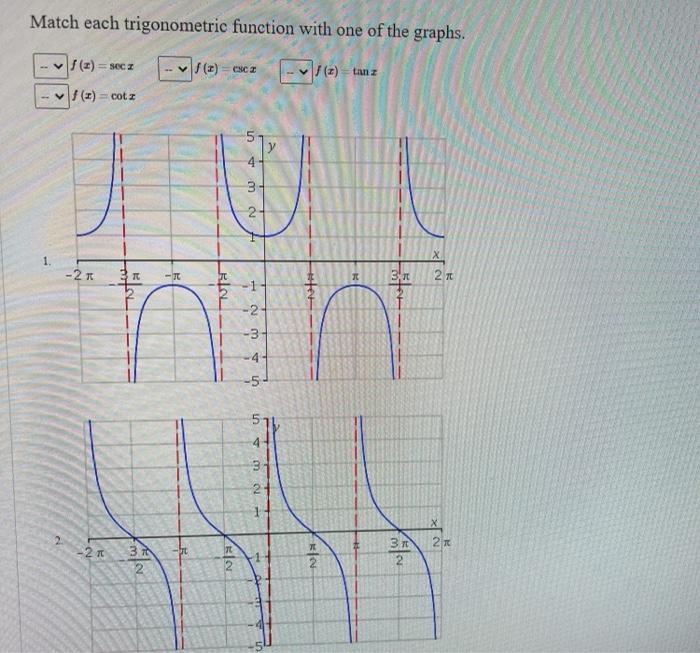
Match each trigonometric function with one of the graphs. – In the realm of trigonometry, the interplay between trigonometric functions and their graphical representations unfolds as a captivating dance of mathematical precision. This exploration delves into the depths of sine, cosine, tangent, cosecant, secant, and cotangent, unveiling their unique characteristics and the intricate relationship between their properties and the shape of their graphs.
As we embark on this journey, we will uncover the practical applications of trigonometric functions in diverse fields such as navigation, surveying, and engineering. By dissecting the key characteristics of each trigonometric graph, including amplitude, period, phase shift, and vertical shift, we will gain a profound understanding of how these functions manifest visually.
Trigonometric Functions and Their Graphs: Match Each Trigonometric Function With One Of The Graphs.
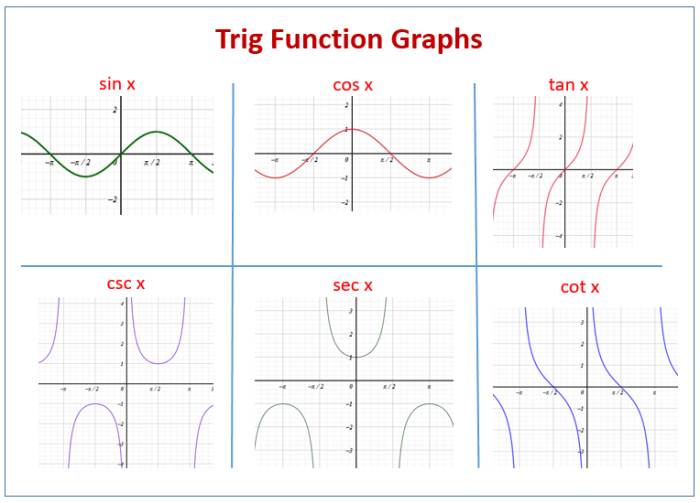
Trigonometric functions are a set of mathematical functions that describe the relationships between the sides and angles of a right triangle. The most common trigonometric functions are sine, cosine, tangent, cosecant, secant, and cotangent.
Trigonometric functions have a wide range of applications in real-world situations, such as navigation, surveying, and engineering. For example, navigators use trigonometric functions to determine the position of a ship at sea, while surveyors use them to measure the distances between objects.
Characteristics of Trigonometric Graphs
Each trigonometric function has its own unique graph. The key characteristics of a trigonometric graph include:
- Amplitude: The amplitude of a trigonometric function is the distance between the maximum and minimum values of the function.
- Period: The period of a trigonometric function is the distance between two consecutive peaks or troughs of the function.
- Phase shift: The phase shift of a trigonometric function is the horizontal displacement of the graph from its original position.
- Vertical shift: The vertical shift of a trigonometric function is the vertical displacement of the graph from its original position.
Matching Trigonometric Functions to Their Graphs, Match each trigonometric function with one of the graphs.
The following table matches each trigonometric function to its corresponding graph:
| Trigonometric Function | Graph |
|---|---|
| Sine |  |
| Cosine |  |
| Tangent |  |
| Cosecant |  |
| Secant |  |
| Cotangent |  |
Relationship between Trigonometric Functions and Their Graphs
The properties of a trigonometric function determine the shape of its graph. For example, the amplitude of a trigonometric function determines the height of its peaks and troughs, while the period of a trigonometric function determines the distance between its peaks and troughs.
The phase shift and vertical shift of a trigonometric function determine the horizontal and vertical displacement of its graph, respectively.
Essential Questionnaire
What are the key characteristics of trigonometric graphs?
The key characteristics include amplitude, period, phase shift, and vertical shift.
How are trigonometric functions used in real-world applications?
Trigonometric functions are used in navigation, surveying, engineering, and many other fields.
What is the relationship between the properties of trigonometric functions and the shape of their graphs?
The properties of trigonometric functions, such as amplitude and period, directly affect the shape of their graphs.